Die in diesem Projekt von der AG „Resonante Röntgenmethoden und Kristallmodellierung“ zusammen mit Emeritus Prof. Karl Fischer (Saarbrücken) verfolgte Methodik zur Kristallstrukturbestimmung wurde innerhalb der letzten 15 Jahre durch K. Fischer, A. Kirfel und H. Zimmermann theoretisch ausgearbeitet, bis hin zur Anwendung formuliert und bereits an zahlreichen Beispielen für teilweise herausfordernde Probleme der Strukturlösung getestet.

Allgemein ist die Kristallstrukturbestimmung aus Beugungsdaten in vielen Bereichen der Festkörper­forschung, wie z. B. der Physik, der Chemie, der Mineralogie und den Materialwissenschaften bis hin zur Biologie und Pharmazie, eine fundamentale Basis um Eigenschaften von Materialien sowie deren Wirkung und Funktionalität zum einen verstehen und zum anderen gezielt modifizieren zu können. Die entsprechenden Datenbanken wachsen jährlich um mehrere zehntausend Strukturen. Die State-of-the-art-Methodik zur Bestimmung von Kristallstrukturen beruht dabei auf Fourier-Transformationen der streuenden Dichte (z. B. Elektronendichte für die Röntgendiffraktion, Kerndichte für die Neutronendiffraktion). Hierbei ist die experimentelle Datenbasis im Allgemeinen unvollständig, da nur die quadratischen Amplituden der Fourier-Koeffizienten, also der Strukturfaktoren über die Reflexionsintensitäten, nicht aber ohne weiteres ihre Phasen erfassbar sind (Phasenproblem der Kristallographie). Die experimentelle Phasenbestimmung, z. B. über resonante Streumethoden, ist sowohl aufwendiger als auch anspruchsvoller. Es gibt etablierte Methoden, um die Phasen mit zusätzlichem Wissen über die Eigenschaften der zu rekonstruierenden Dichte (Positivität, Spitzigkeit) zu gewinnen und die Struktur zu lösen, u. a. die so genannten direkten Methoden, die Patterson-Methode und die isomorphe Substitution.

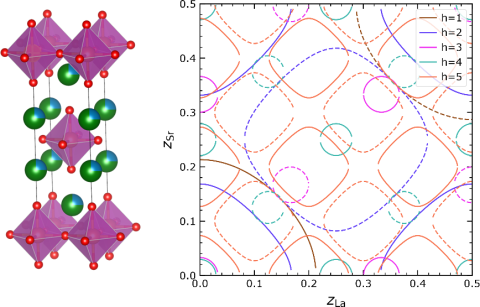
Während aktuelle Methoden zur Bestimmung der atomistischen Kristallstruktur umfangreiche Informationen über die vom Kristall gebeugten Röntgenwellen, sog. Reflexe, benötigen, hat das neue Konzept einen entscheidenden Vorteil: Es müssen weniger Reflexe im Kristall gemessen werden, um ein qualitativ hochwertigeres Modell zu berechnen. Dank des neuen Ansatzes erhält man unter den Randbedingungen gemessener Reflexintensitäten Hyperflächen, sog. Isoflächen, im hochdimensionalen Parameterraum, die sich an bestimmten Punkten schneiden. Diese Schnittpunkte legen die Positionen jedes Atoms der Elementarzelle fest. Ein weiterer Vorteil ist, dass dafür keine inverse Fouriertransformation benötigt wird. Nachteil der Methode: Für die Lösung hochdimensionaler Parameterproblematiken sind hohe Rechenkapazitäten erforderlich, was die Zahl der strukturellen Freiheitsgrade derzeit begrenzt.

Im Projekt werden verschiedene Ansätze verfolgt, um die Isoflächen im Parameterraum zu beschreiben, die notwendigen Schnitte durchzuführen und das Lösungsvolumen durch Messung ausgewählter Reflexintensitäten optimal zu begrenzen. Ein speichersparender Ansatz ist die lineare Parametrisierung der Isoflächen, ein speicherintensiver die Grid-basierte Berechnung der Flächen.