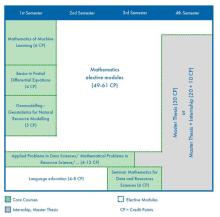
Mathematics for Data and Resource Sciences
Mathematical skills are indispensable in today's activities of modern industrial companies. In addition, the necessary quantification, proper assessment and recording of the content of application-orientated research can only be achieved through a high and qualified use of mathematical methods. Particularly in view of climate change and in addressing the associated challenges, the processing of large amounts of data on the one hand and the understanding of technical difficulties in the provision, transport, and recycling of recyclable materials on the other are essential. Based on an excellent mathematical foundation, ideally laid in a general bachelor's degree program in mathematics, the English-language Mathematics for Data and Resource Sciences degree program focuses on the methods and techniques needed to understand and mathematically tackle the challenges described above.
Aim of the degree program
Successful graduates of the Mathematics for Data and Resource Sciences Master's degree program have the techniques, methods, and general mathematical skills to solve today's most pressing problems. This includes understanding and utilizing large amounts of data, mastering computer-aided machine learning and a thorough understanding of problems in the area of scarce resources, such as rare raw materials in particular or planet Earth in general.
Application-oriented lecture series
Mathematical problems from practice are discussed in lecture series created specifically for the degree program. These provide a catalog of relevant problems in order to apply the skills learned in a meaningful way. The topics presented relate to the core of the individual research areas and are constantly updated in order to gain the best insight into the mathematical issues.
Industrial internship
Students are rewarded for their commitment to local companies. If you complete an industrial internship lasting at least four months during your degree program, this time can be credited towards your Master's thesis: The maximum completion time is reduced by 3 months to 6 months and the required content is lowered accordingly. In particular, this is intended to benefit the local economy through quick graduation and the students' tailored skills on the one hand and the students themselves through a permanent employment relationship in the region at best.
Study-related Master's thesis
This degree program offers a wide range of courses. This guarantees a very comprehensive and multi-faceted education. In order to be able to extend the diverse content to all four Master's semesters, the Master's thesis can already begin during the third semester thanks to more flexible deadlines than in most other degree programs.
Certification for special training
It is possible to obtain certification as part of the international Master's program if you have acquired in-depth knowledge in Mathematical Data Science or Geomathematics during your studies. Thanks to the respective specialization, with the first focusing more on the processing and handling of (large) amounts of data and the second focusing more on mathematical problems of climate change or the circular economy, graduates are ideally prepared for the demands of professional practice.
Please note that this is an English-language Master's degree programme. Applications can be submitted online via the university portal and are possible from 1 January to 15 April.
- Faculty
-
Faculty of Mathematics and Computer Science (Faculty 1)
- Degree
-
Master of Science (M. Sc.)
- Standard period of study
-
4 Semester
- Part-time possible
-
No
- Start of studies
-
Winter semesterSummer semester
- Admission requirement
-
- B. Sc. in Mathematics or comparable
- Qualification interview
- Letter of motivation (one A4 page)
Language skills:
- TOEFL min. 90 points (internet-based test) or
- IELTS min. 6.5 or equivalent language test or
- a university entrance qualification obtained at an English-speaking school, a degree programme taught entirely in English or English as a native language (can be taken into account as an equivalent)
- Course language
-
English
- IT companies such as Google or IBM
- Financial industry and insurance: e.g. in data analysis
- Circular economy: e.g. in the optimisation of software for wastewater treatment plants, resource optimisation in industrial manufacturing processes or in materials science
- Corporate consulting: e.g. in data analysis
- Automotive industry: e.g. in the field of autonomous driving or software validation
Why study Mathematics for Data and Resource Sciences at TUBAF?
Studying at TUBAF is interesting
- Classical, solid basic education
- A wide range of application-oriented specialisations
- Theses also possible in cooperation with industry and business
- Student exchange with partner universities in Europe, Canada and the U.S.A.
Studying at TUBAF is effective
- Efficient study and timetables and timetables tailored to the standard period of study
- Exceptionally good supervision ratio
- Intensive contact between lecturers and students
Studying at TUBAF is individual
- At TUBAF, the professor knows the students personally
- Individual solutions are developed for any problems that arise during studies
- Adaptation of specialisation and application subjects to personal inclinations and abilities
Studying at TUBAF is exclusive
- The combination of classical basic mathematical subjects with a broad range of applications is unique in Germany
- Many attractive application areas
- Highest quality of education by proven and committed professors
Required prior knowledge
Analysis
Essential
- Continuity
- Differentiability
- Integrability
- Functions of more than one variables
- Metric Spaces
- Implicit Function Theorem
- Criteria for Existence and Uniqueness of Ordinary Differential Equations
Desirable:
- Banach spaces
- Hilbert Spaces
- Compactness
- Hahn-Banach Theorem
- Open Mapping Theorem
- Manifolds
- L_p-spaces
Discrete Mathematics/Algebra
Essential:
- set-theoretic and logical foundations
- order theory
- algebraic structures and homomorphisms
- linear algebra (vector spaces, linear operators, duality theory, eigenvalues)
Desirable:
- basics of graph theory and combinatorics
Numerics
Essential:
- Newton's method
- direct and iterative methods for linear systems of equations
- least squares problems
- interpolation using polynomials
- numerical integration using Newton-Cotes
- fluency in one programming language (e. g. Python, Matlab, C/C++, Fortran)
Desirable:
- Newton's method in higher dimensions
- .g. Python, Matlab, C/C++, Fortran)
Desirable:
- Newton's method in higher dimensions
- Gauss integration
- Matlab or Python programming
Optimisation
Essential:
- Simplex algorithm
- duality in linear programming
- separation theorems
- KKT conditions
- constraint qualifications
- sufficient optimality conditions
- Lagrange duality
Desirable:
- optimality conditions for convex optimisation problems
- Newton's algorithm
- gradient descent methods
- penalty methods
- optimisation on graphs
Stochastics
Essential:
- Probability measure and sigma algebra
- Distribution functions and moments
- Random variables
- Conditional probability
- Law of large numbers and central limit theorem
- Estimators and confidence intervals
- Statistical hypothesis testing
- Linear regression
Desirable:
- Measure theory
- Conditional expectation
- Stochastic processes