Mathematics for Data and Resource Sciences
In heutigen Tätigkeiten von modernen Industrieunternehmen sind mathematische Fähigkeiten unumgänglich. Zudem sind die notwendige Quantifizierung, sachgemäße Beurteilung und Erfassung der Inhalte anwendungsorientierter Forschung nur durch einen hohen und qualifizierten Einsatz mathematischer Methoden durchführbar. Insbesondere angesichts des Klimawandels sowie auch bei der Adressierung der damit verbundenen Herausforderungen sind die Verarbeitung großer Datenmengen einerseits und das Verständnis technischer Schwierigkeiten im Bereitstellen, Befördern, und Recyceln von Wertstoffen andererseits essentiell. Basierend auf einem hervorragenden mathematischen Fundament, das idealerweise in einem allgemeinbildenden Bachelorstudiengang Mathematik gelegt wurde, fokussiert sich der englischsprachige Studiengang Mathematics for Data and Resource Sciences auf die Methoden und Techniken, um die obenbeschriebenen Herausforderungen zu verstehen und mathematisch angehen zu können.
Ziel des Studiengangs
Erfolgreiche Absolventinnen und Absolventen des Masterstudiengangs Mathematics for Data and Resource Sciences verfügen über die Techniken, Methoden und die allgemeinen mathematischen Fähigkeiten, um die drängendsten Probleme der heutigen Zeit lösen zu können. Dazu gehören das Verständnis und die Verwertbarkeit großer Datenmengen, das Beherrschen des computergestützten sogenannten maschinellen Lernens sowie ein großes Problemverständnis im Bereich knapper Ressourcen, wie seltener Rohstoffe im Speziellen oder dem Planeten Erde im Allgemeinen.
Anwendungsorientierte Ringvorlesungen
In eigens für den Studiengang erstellten Ringvorlesungen werden mathematische Probleme aus der Praxis diskutiert. Diese liefern einen Katalog relevanter Problemstellungen, um die erlernten Fähigkeiten sinnvoll anzuwenden. Dabei betreffen die vorgestellten Themenkomplexe den Kern der einzelnen Forschungsgebiete und werden ständig aktualisiert, um den besten Einblick in die mathematischen Fragestellungen zu gewinnen.
Industriepraktikum
Ein Engagement der Studierenden bei lokal ansässigen Firmen wird belohnt. Absolviert man während des Studiums ein mindestens vier Monate andauerndes Industriepraktikum, kann diese Zeit auf die Bearbeitung der Masterarbeit angerechnet werden: Die maximale Bearbeitungsdauer wird um 3 Monate auf 6 Monate verkürzt und der erforderliche Inhalt entsprechend abgesenkt. Insbesondere soll dadurch die lokale Wirtschaft von schnellen Abschlüssen und passgenauen Fähigkeiten der Studierenden einerseits als auch die Studierenden selbst durch ein bestenfalls dauerhaftes Arbeitsverhältnis in der Region profitieren.
Studienbegleitende Masterarbeit
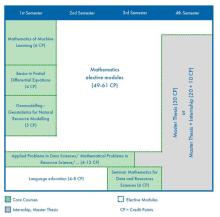
Das Studienangebot im vorliegenden Studiengang ist breit gefächert. Dadurch kann eine sehr umfassende und facettenreiche Ausbildung garantiert werden. Um die vielfältigen Inhalte auf alle vier Mastersemester ausdehnen zu können, kann die Bearbeitung der Masterarbeit durch flexiblere Fristen als bei den meisten anderen Studiengängen schon während des 3. Semesters beginnen.
Zertifizierung für spezielle Ausbildung
Im Rahmen des internationalen Masters ist es möglich, sich zertifizieren zu lassen, wenn während des Studiums vertiefte Kenntnisse in Mathematical Data Science oder Geomathematics erlangt wurden. Durch die jeweilige Spezialisierung, wobei die erste eher den Fokus auf die Ver- und Bearbeitung (großer) Datenmengen legt und die zweite eher mathematische Probleme des Klimawandels oder der Kreislaufwirtschaft ins Zentrum des Interesses stellt, sind Absolventen und Absolventinnen ideal für die Anforderungen in der beruflichen Praxis vorbereitet.
Bitte beachten Sie, dass es sich um einen englischsprachigen Master-Studiengang handelt. Die Bewerbung erfolgt online über das Hochschulportal und ist möglich im Zeitraum vom 1. Januar bis 15. April.
- Fakultät
-
Fakultät 1 - Mathematik und Informatik
- Abschluss
-
Master of Science (M. Sc.)
- Regelstudienzeit
-
4 Semester
- Teilzeit möglich
-
Nein
- Studienbeginn
-
WintersemesterSommersemester
- Zulassungsvoraussetzung
-
- B. Sc. in Mathematik oder vergleichbar
- Qualifikationsfeststellungsgespräch
- Motivationsschreiben (eine A4-Seite)
Sprachkenntnisse:
- TOEFL min. 90 Punkte (Internet-basierter Test) oder
- IELTS min. 6.5 oder äquivalenter Sprachtest oder
- eine an einer englischsprachigen Schule erworbene Hochschulzugangsberechtigung, ein vollständig englischsprachiges Studium oder die englische Sprache als Muttersprache (diese können als Äquivalent angerechnet werden)
- Studiengangsprache
-
Englisch
- IT-Unternehmen wie z.B. Google oder IBM
- Finanzindustrie und Versicherung: z.B. in der Datenanalyse
- Kreislaufwirtschaft: z.B. bei der Optimierung von Software für Kläranlagen, der Ressourcenoptimierung bei industriellen Fertigungsprozessen oder auch in den Materialwissenschaften
- Unternehmensberatung: z.B. in der Datenanalyse
- Automobilindustrie: z.B. im Bereich des autonomen Fahrens oder der Absicherung von Software
Warum Mathematics for Data and Resource Sciences an der TUBAF studieren?
Das Studium an der TUBAF ist interessant
- klassische, solide Grundlagenausbildung
- vielfältige anwendungsorientierte Vertiefungsrichtungen
- Abschlussarbeiten auch in Kooperation mit Industrie und Wirtschaft möglich
- Studierendenaustausch mit Partneruniversitäten in Europa, Kanada und den U.S.A.
Das Studium an der TUBAF ist effektiv
- effiziente Studien- und Stundenpläne abgestimmt auf die Regelstudienzeit
- außergewöhnlich gutes Betreuungsverhältnis
- intensiver Kontakt zwischen Lehrenden und Studierenden
Das Studium an der TUBAF ist individuell
- an der TUBAF kennt die Professorin/der Professor die Studierenden persönlich
- für auftretende Probleme im Studium werden individuelle Lösungen erarbeitet
- Anpassung von Vertiefung und Anwendungsfächern an persönliche Neigungen und Fähigkeiten
Das Studium an der TUBAF ist exklusiv
- vorhandene Kombination der klassischen mathematischen Grundlagenfächer mit dem breiten Anwendungsspektrum ist einzigartig in Deutschland
- viele attraktive Anwendungsbereiche
- höchste Qualität der Ausbildung durch ausgewiesene und engagierte Professor:innen
Erforderliche Vorkenntnisse
Analysis
Essentiell:
- Stetigkeit
- Differentierbarkeit
- Integrierbarkeit
- Funktionen mehrerer Veränderlicher
- Metrische Räume
- Satz von der impliziten Funktion
- Kriterien für die eindeutige Lösbarkeit gewöhnlicher Differentialgleichungen
Wünschenswert:
- Banachräume
- Hilberträume
- Kompaktheit
- Satz von Hahn—Banach
- Satz von der offenen Abbildung
- Mannigfaltigkeiten
- Lebesgueräume
Diskrete Mathematik/Algebra
Essentiell:
- Mengentheoretische und aussagenlogische Grundlagen
- Ordnungsrelationen
- Algebraische Strukturen und Homomorphismen
- Lineare Algebra (Vektorräume, lineare Operatoren, Dualräume, Eigenwerte)
Wünschenswert:
- Grundlagen der Graphentheorie und Kombinatorik
Numerische Mathematik
Essentiell:
- Newton-Methode
- Direkte und iterative Methoden für lineare Gleichungssysteme
- Ausgleichsrechnung
- Interpolation mit Polynomen
- Numerische Integration mittels Newton-Cotes
- Beherrschung einer Programmiersprache (z.B. Python, Matlab, C/C++, Fortran)
Wünschenswert:
- Newton-Verfahren in höheren Dimensionen
- Gauß-Integration
- Matlab- oder Python-Programmierung
Optimierung
Essentiell:
- Simplex-Algorithmus
- Dualität in der linearen Optimierung
- Trennbarkeitssätze
- Karush-Kuhn-Tucker-Bedingungen
- Constraint qualifications
- hinreichende Optimalitätsbedingungen
- Lagrange-Dualität
Wünschenswert:
- Optimalitätsbedingungen für konvexe Optimierungsprobleme
- Newton-Verfahren
- Gradientenabstiegsverfahren
- Strafverfahren
- Optimierung auf Graphen
Stochastik
Essentiell:
- Wahrscheinlichkeitsmaß und Sigma-Algebra
- Zufallsvariablen
- Verteilungsfunktionen und Momente
- Bedingte Wahrscheinlichkeit
- Gesetz der großen Zahlen und zentraler Grenzwertsatz
- Schätzer und Konfidenzintervalle
- Statistische Hypothesentests
- Lineare Regression
Wünschenswert:
- Maßtheorie
- Bedingte Erwartung
- Stochastische Prozesse